Oppslag, diagrammer, statistikk og pivottabeller

Etter å ha gjennomgått grunnleggende funksjoner, cellehenvisninger og dato- og tidsfunksjoner, dykker vi nå inn i noen av de mer avanserte funksjonene i Microsoft Excel. Vi presenterer metoder for å løse klassiske problemer i finans, salgsrapporter, fraktkostnader og statistikk.
SCHOOL NAVIGASJON- Hvorfor trenger du formler og funksjoner?
- Definere og opprette en formel
- Relativ og Absolutt Cellreferanse, og Formatering
- Nyttige funksjoner du bør bli kjent med
- Oppslag, diagrammer, statistikk og pivottabeller
Disse funksjonene er viktige for bedrifter, studenter og de som bare vil lære mer.
VLOOKUP og HLOOKUP
Her er et eksempel for å illustrere vertikale oppslag (VLOOKUP) og horisontale oppslag (HLOOKUP) -funksjoner. Disse funksjonene brukes til å oversette et tall eller en annen verdi til noe som er forståelig. For eksempel kan du bruke VLOOKUP til å ta et delenummer og returnere elementbeskrivelsen.
For å undersøke dette, la oss gå tilbake til "Decision Maker" -skjemaet i del 4, der Jane prøver å bestemme hva som skal brukes på skolen. Hun er ikke lenger interessert i det hun har, siden hun har landet en ny kjæreste, så hun vil nå ha tilfeldige antrekk og sko.
I Janes regneark viser hun antrekk i vertikale kolonner og sko, horisontale kolonner.
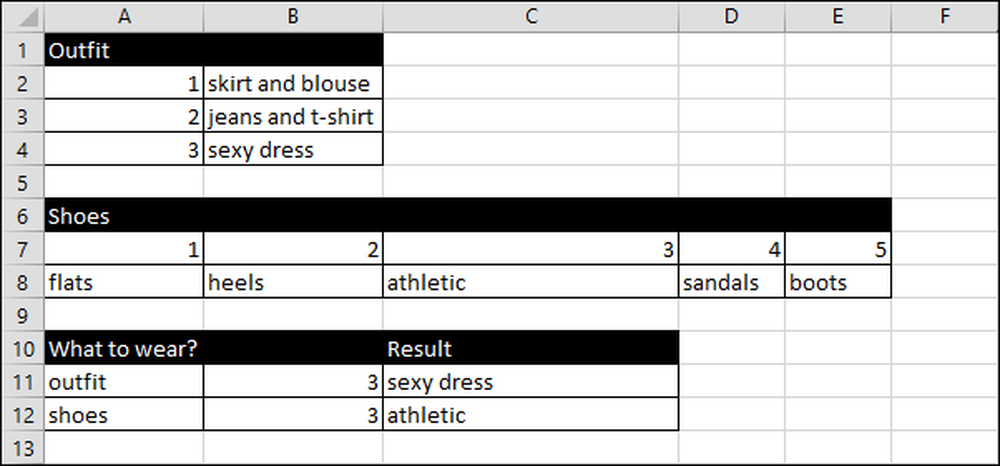
Hun åpner regnearket og funksjonen RANDBETWEEN (1,3) genererer et tall mellom eller lik en og tre som svarer til de tre typer antrekk hun kan ha på seg.
Hun bruker funksjonen RANDBETWEEN (1,5) for å velge mellom fem typer sko.
Siden Jane ikke kan bruke et nummer, må vi konvertere dette til et navn, så vi bruker oppslagsfunksjoner.
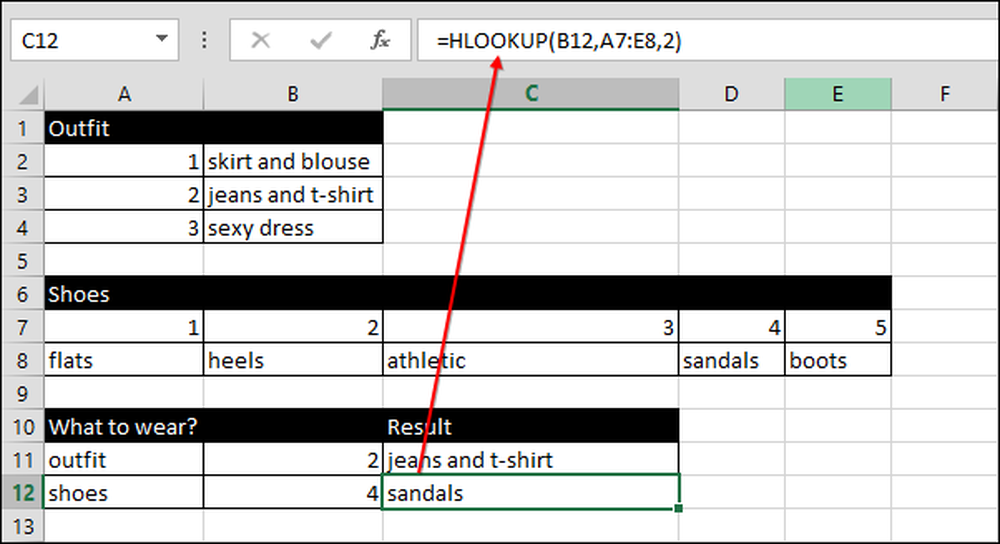
Vi bruker VLOOKUP-funksjonen til å oversette antrekknummeret til antrekknavnet. HLOOKUP oversetter fra skonnummer til de forskjellige typer sko på rad.
Regnearket fungerer som dette for antrekk:

Excel plukker et tilfeldig tall fra en til tre, siden hun har tre antrekkalternativer.
Deretter oversetter formelen tallet til tekst ved hjelp av = VLOOKUP (B11, A2: B4,2) som bruker tilfeldig tall verdien fra B11 til å se i området A2: B4. Den gir deretter resultatet (C11) fra dataene som er oppført i den andre kolonnen.
Vi bruker samme teknikk for å plukke sko, bortsett fra denne gangen bruker vi VOOKUP i stedet for HLOOKUP.
Eksempel: Grunnleggende statistikk
Nesten alle vet en formel fra statistikk - gjennomsnittlig - men det er en annen statistikk som er viktig for virksomheten: standardavvik.
For eksempel, mange en person som har gått på college har agonized over deres SAT score. De vil kanskje vite hvordan de rangerer i forhold til andre studenter. Universitetene vil også vite dette fordi mange universiteter, særlig prestisjetunge, slår ned studenter med lave SAT-poeng.
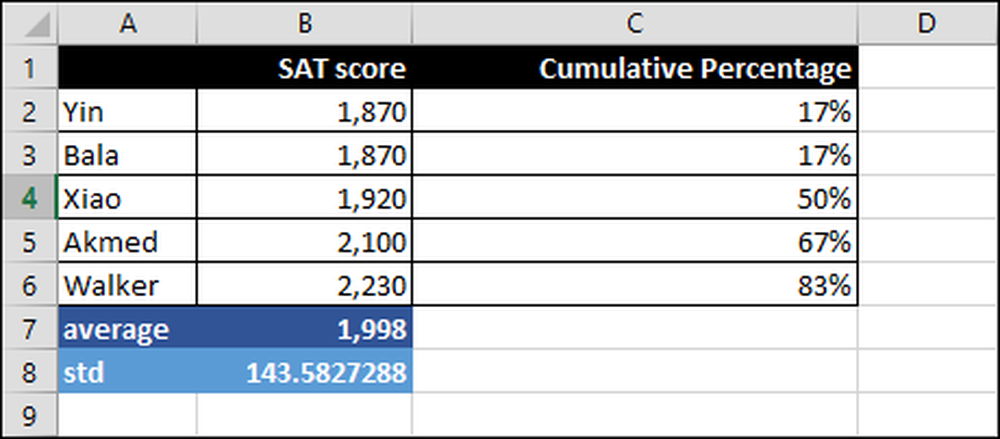
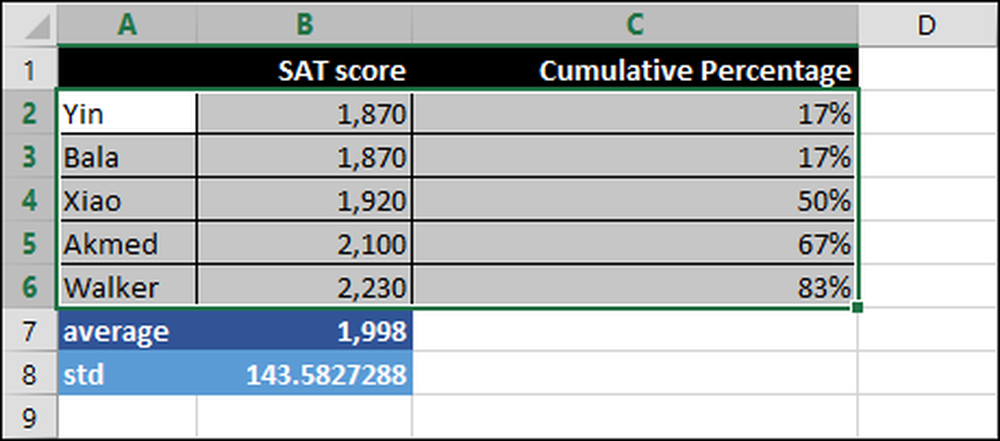
Så hvordan skal vi, eller et universitet, måle og tolke SAT-score? Nedenfor er SAT-poengsum for fem studenter fra 1,870 til 2,230.
De viktige tallene å forstå er:
Gjennomsnitt - Gjennomsnitt er også referert til som "mean".
Standardavvik (STD eller σ) - Dette tallet viser hvor stort spredt et sett med tall er. Hvis standardavviket er stort, er tallene langt fra hverandre, og hvis det er null, er alle tallene det samme. Du kan si at standardavviket er gjennomsnittlig forskjell mellom gjennomsnittsverdien og den observerte verdien, dvs. 1,998 og hver SAT-poengsum. Vær oppmerksom på at det er vanlig å forkorte standardavviket ved hjelp av det greske symbolet sigma "σ."
Prosentlig rangering - Når en student får en høy poengsum, kan de skryte av at de er i topp 99 prosentilen eller noe sånt. "Percentile rang" betyr prosentandelen av poengene er lavere enn en bestemt score.
Standardavvik og sannsynlighet er nært knyttet. Du kan si at for hver standardavvik, er sannsynligheten eller sannsynligheten for at tallet ligger innenfor det antallet standardavvik som er:
| STD | Andel av poeng | Utvalg av SAT-poeng |
| 1 | 68% | 1,854-2,142 |
| 2 | 95% | 1,711-2,285 |
| 3 | 99,73% | 1,567-2,429 |
| 4 | 99,994% | 1,424-2,572 |
Som du kan se, er sjansen for at noen SAT-score er utenfor 3 STD'er praktisk talt null fordi 99,73 prosent av resultatene er innenfor 3 STDs.
La oss nå se på regnearket igjen og forklare hvordan det fungerer.
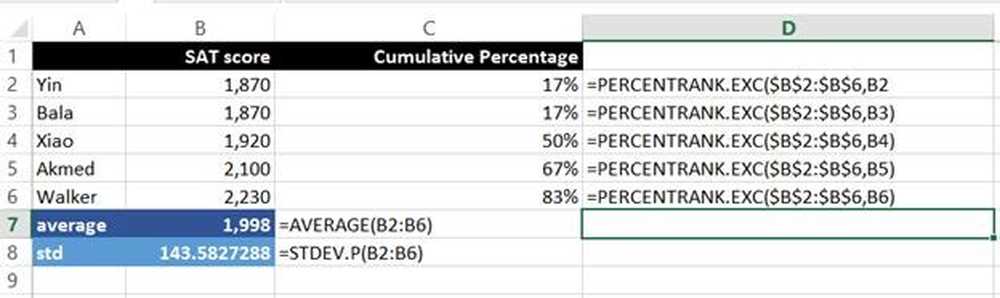
Nå forklarer vi formlene:
= Gjennomsnitt (B2: B6)
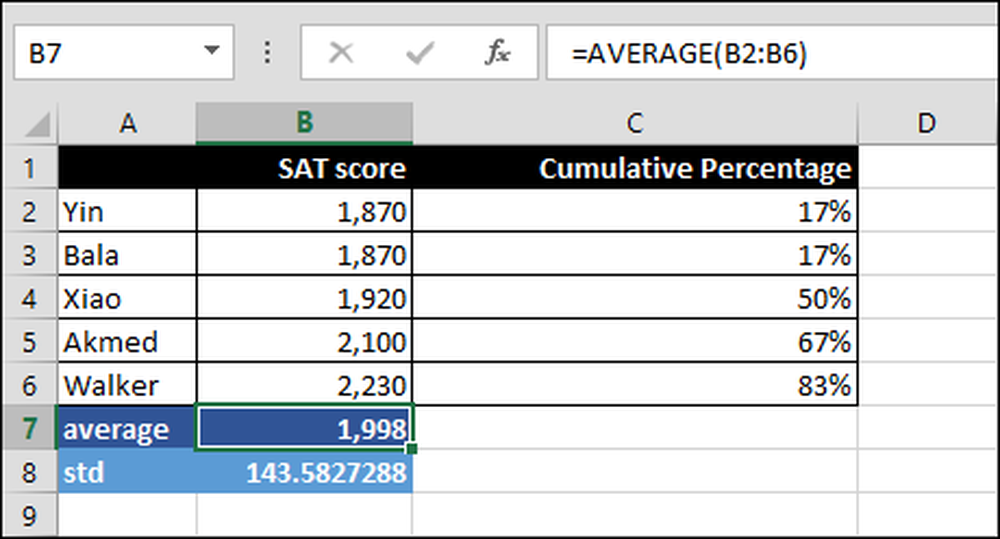
Gjennomsnittet av alle poengene over rekkevidde B2: B6. Spesifikt summen av alle delene delt på antall personer som tok testen.
= STDEV.P (B2: B6)
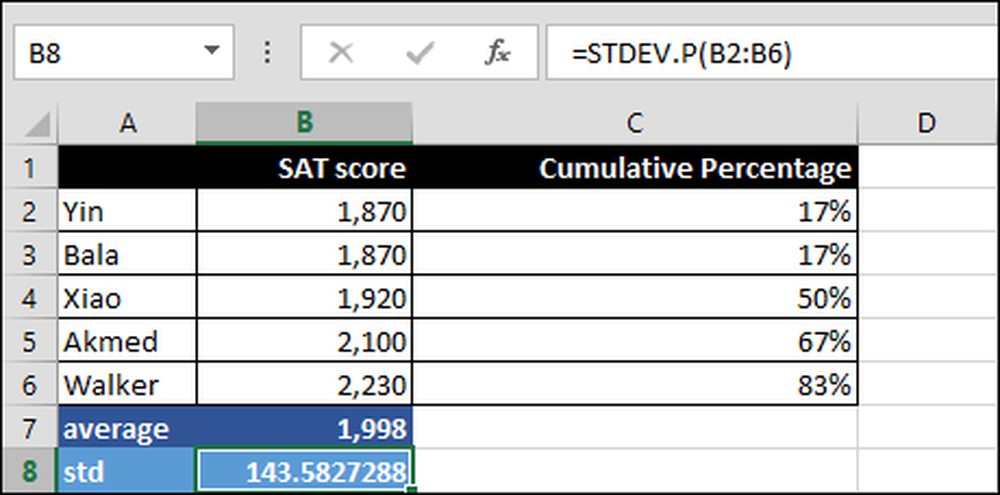
Standardavviket over rekkevidde B2: B6. ".P" betyr STDEV.P brukes over alle poengene, dvs. hele befolkningen og ikke bare en delmengde.
= PERCENTRANK.EXC ($ B $ 2: $ B $ 6, B2)
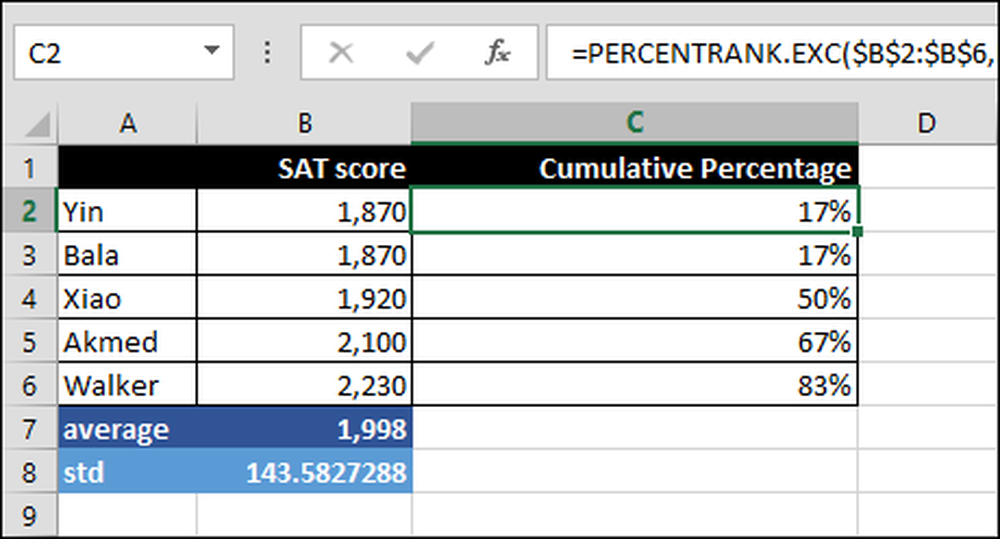
Dette beregner den kumulative prosentandelen over området B2: B6 basert på SAT-poengsummen, i dette tilfellet B2. For eksempel er 83 prosent av resultatene under Walker's poengsum.
Grafering av resultatene
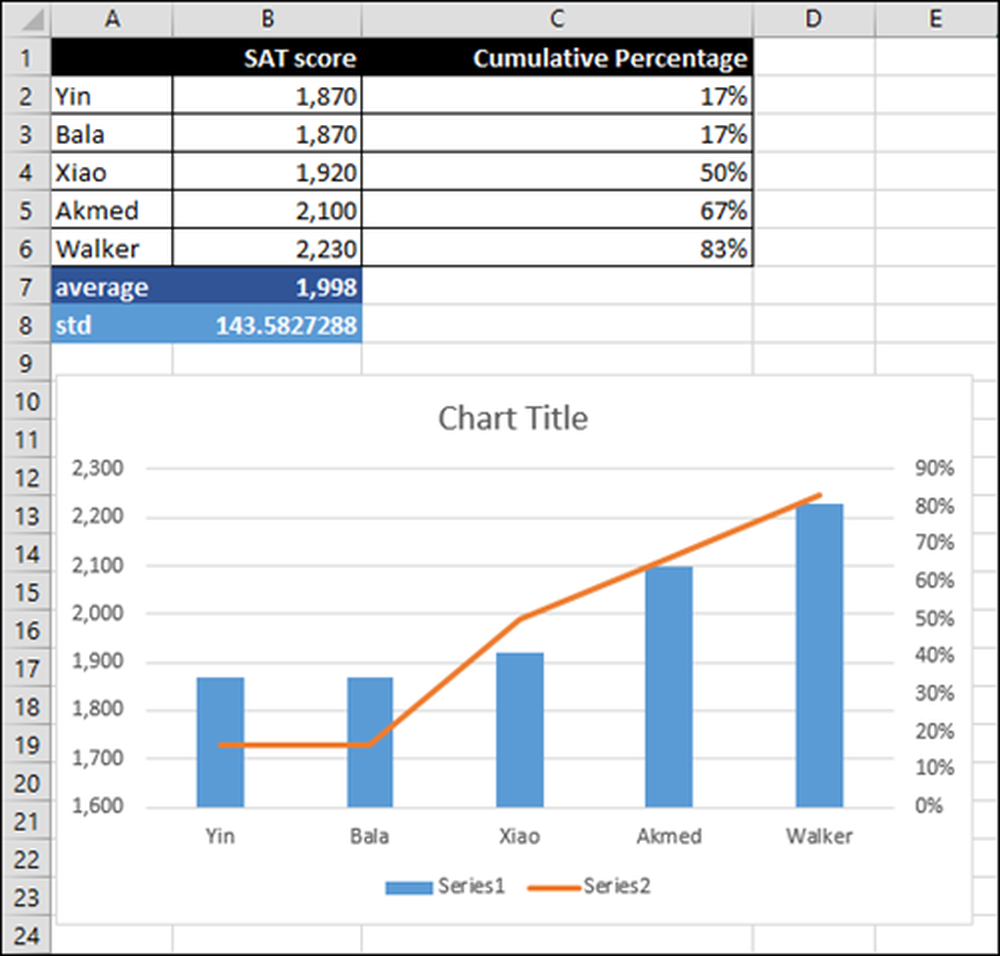
Å sette resultatene i en graf gjør det lettere å forstå resultatene, pluss at du kan vise det i en presentasjon for å gjøre poenget ditt tydeligere.
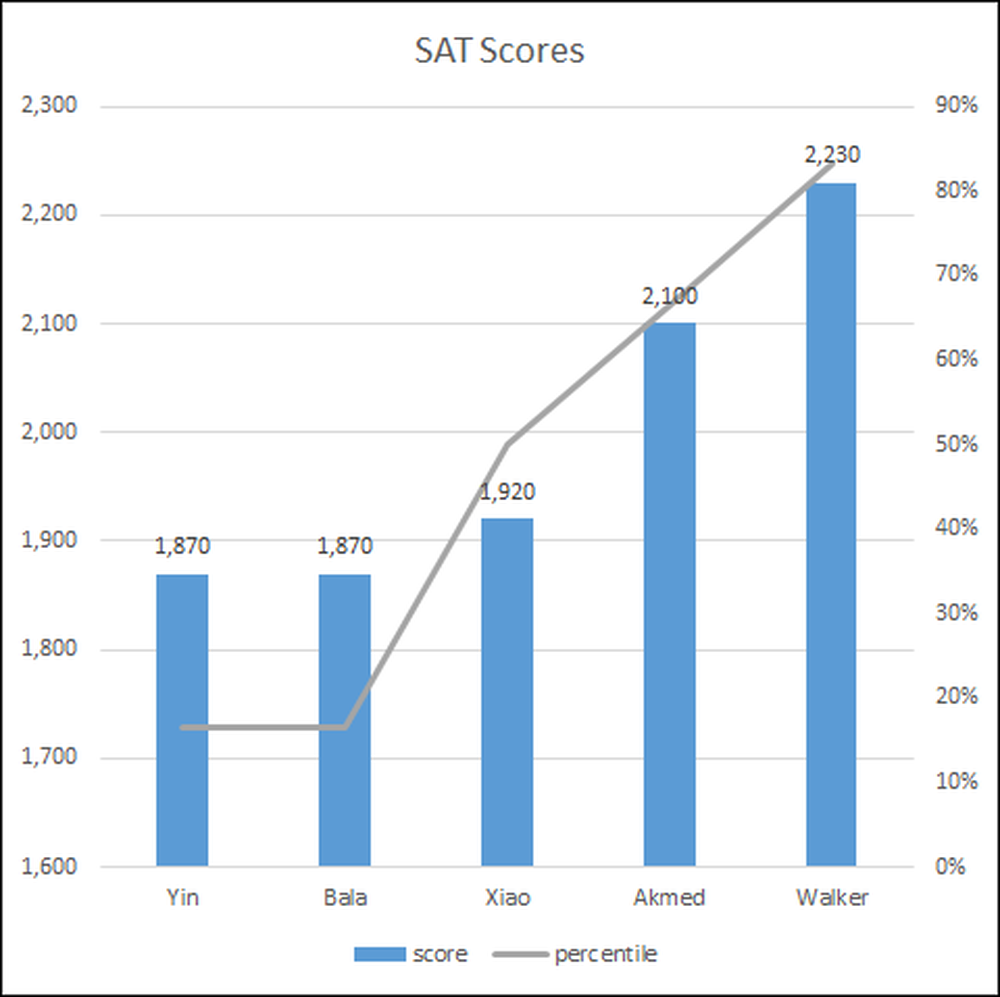
Studentene er på den horisontale akse og deres SAT-poeng blir vist som en blå stanggraf på en skala (vertikal akse) fra 1600 til 2300.
Den prosentvise rangering er den høyre vertikale aksen fra 0 til 90 prosent, og representeres av den grå linjen.
Slik lager du et diagram
Å lage et diagram er et emne for seg selv, men vi vil kort forklare hvordan diagrammet ovenfor ble opprettet.
Først, velg rekkefølge av celler som skal være i diagrammet. I dette tilfellet A2 til C6 fordi vi vil ha tallene så vel som studentens navn.
Fra "Sett inn" -menyen velg "Diagrammer" -> "Anbefalte diagrammer":

Datamaskinen anbefaler et diagram med "Clustered-Column, Secondary Axis". Den "sekundære akse" delen betyr at den trekker to vertikale akser. I dette tilfellet er dette diagrammet det vi ønsker. Vi trenger ikke å gjøre noe annet.

Du kan bruke flytte kartet og omforme det til du har det som størrelse og i ønsket stilling. Når du er fornøyd, kan du lagre diagrammet i regnearket.
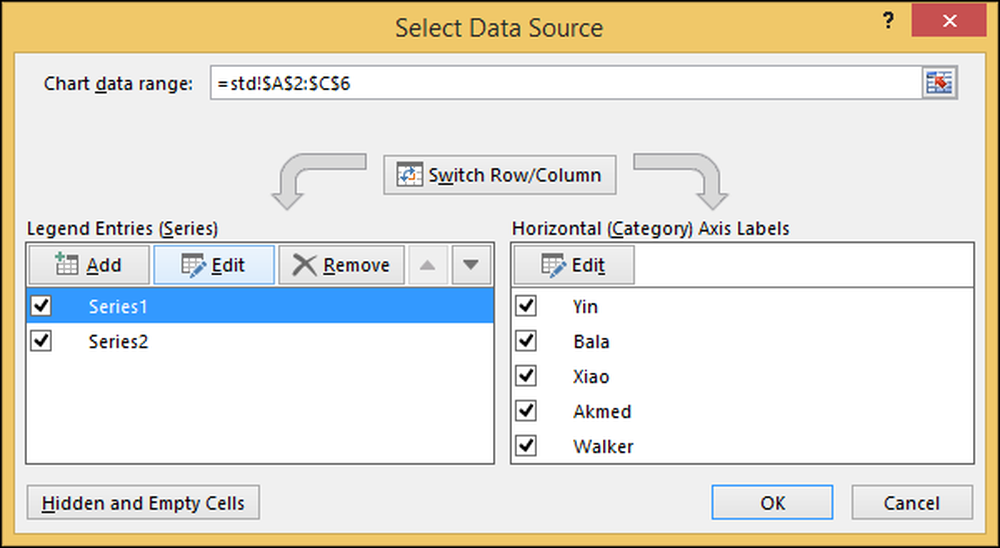
Hvis du høyreklikker på diagrammet, velger du "Velg data", hvilken data som er valgt for området.
Funksjonen "Anbefalte diagrammer" gjør deg vanligvis utilgjengelig for å håndtere så kompliserte detaljer som å bestemme hvilke data som skal inkluderes, hvordan du tilordner etiketter og hvordan du tilordner venstre og høyre vertikale akser.
I dialogboksen "Velg datakilde" klikker du på "poeng" under "Legend Entries (Series)" og trykker "Rediger", og endrer den for å si "Score."
Endre deretter serie 2 ("percentile") til "Percentile."
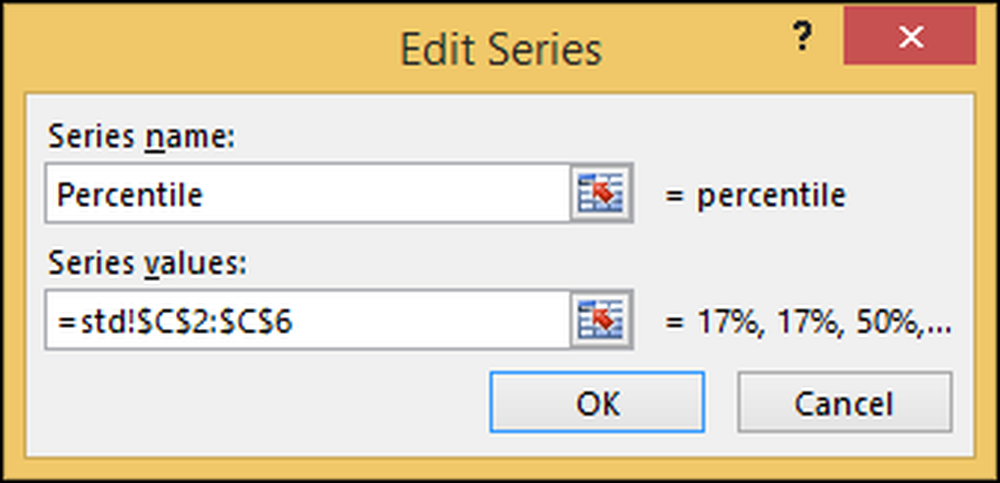
Gå tilbake til diagrammet ditt og klikk på "Chart Title" og endre det til "SAT Scores." Nå har vi et komplett diagram. Den har to horisontale akser: en for SAT-score (blå) og en for kumulativ prosentandel (oransje).

Eksempel: Transportproblemet
Transportproblemet er et klassisk eksempel på en type matematikk kalt "lineær programmering." Dette lar deg maksimere eller minimere en verdifag til visse begrensninger. Den har mange applikasjoner til mange forretningsproblemer, så det er nyttig å lære hvordan det fungerer.
Før vi begynner med dette eksemplet, må vi aktivere "Excel Solver".
Aktiver Solver Add-In
Velg "File" -> "Options" -> "Add-ins". På bunnen av tilleggsalternativene klikker du på knappen "Gå" ved siden av "Administrer: Excel-tillegg."
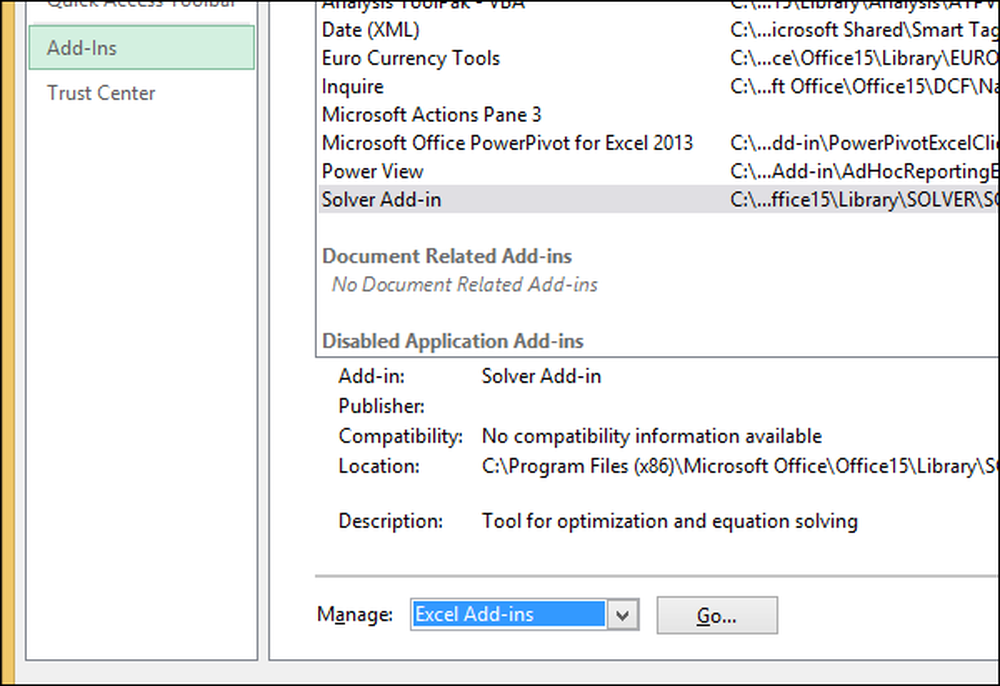
På den resulterende menyen, klikk avkrysningsboksen for å aktivere, "Løs innlasting," og klikk "OK".

Eksempel: Beregn de laveste iPad-fraktkostnadene
Anta at vi leverer iPads, og vi prøver å fylle distribusjonsstedene våre ved å bruke de laveste transportkostnadene. Vi har en avtale med et lastebil og flyselskap for å sende iPads fra Shanghai, Beijing og Hong Kong til distribusjonssentrene vist under.
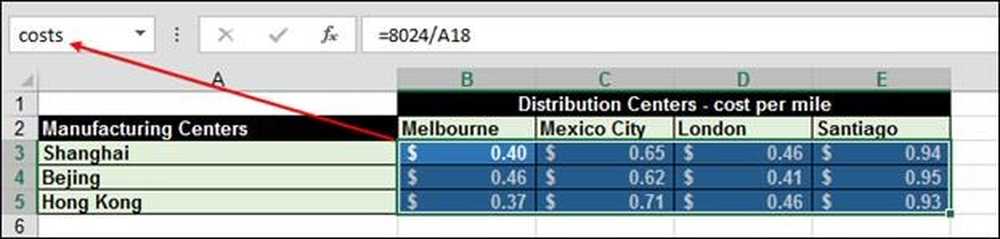
Prisen som sendes hver iPad er avstanden fra fabrikken til distribusjonsstedet til anlegget dividert med 20.000 kilometer. For eksempel er det 8,024 km fra Shanghai til Melbourne, som er 8.024 / 20.000 eller $ .40 per iPad.

Spørsmålet er hvordan sender vi alle disse iPads fra disse tre fabrikkene til disse fire destinasjonene til lavest mulig pris?
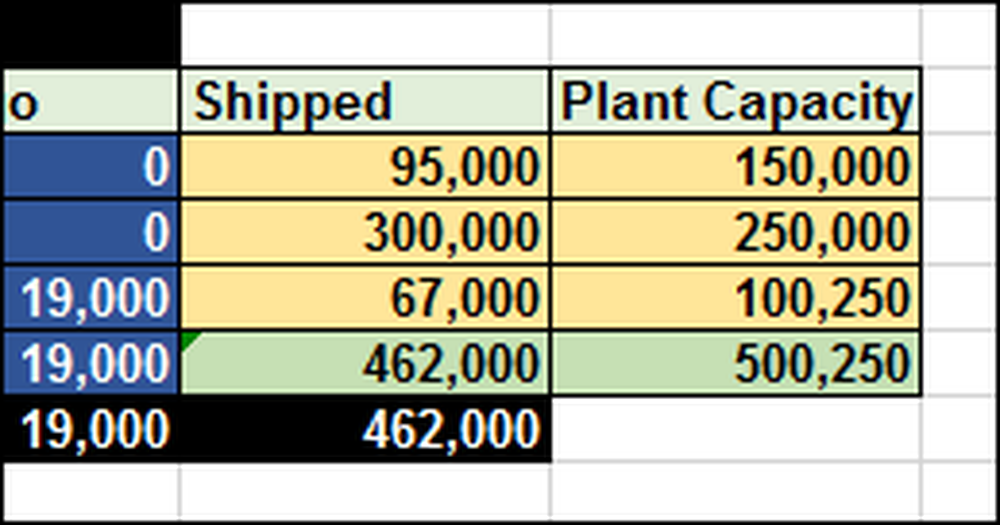
Som du kan forestille deg, kan det være veldig vanskelig å finne ut det uten noen formel og verktøy. I dette tilfellet må vi sende 462 000 (F12) totalt iPads. Anleggene har en begrenset kapasitet på 500 250 (G12) enheter.
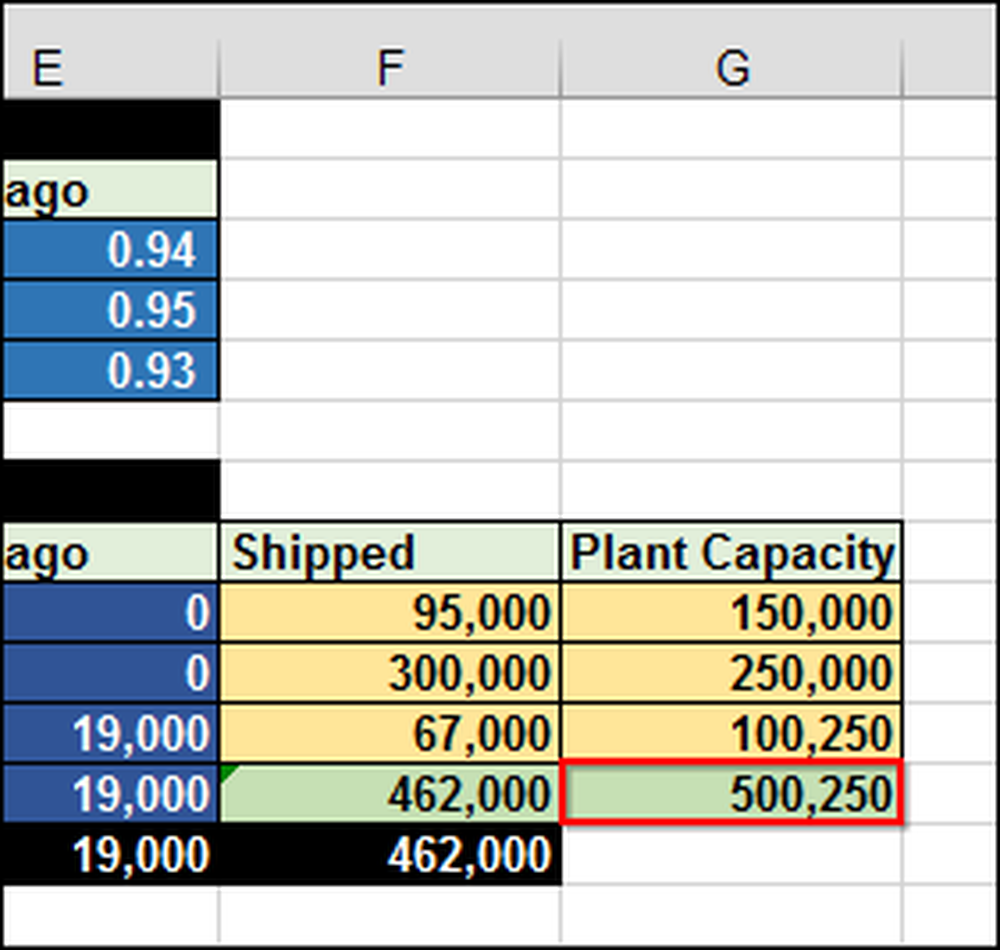
I regnearket, slik at du kan se hvordan det fungerer, har vi skrevet 1 inn i celle B10, noe som betyr at vi ønsker å sende 1 iPad fra Shanghai til Melbourne. Siden transportkostnadene langs den ruten er $ 0,40 per iPad, er den totale kostnaden (B17) $ 0,40.

Tallet ble beregnet ved hjelp av funksjonen = SUMPRODUCT (kostnader, sendt) "kostnader" er rekkeviddeene B3: E5.
Og "sendt" er området B9: E11:

SUMPRODUCT multipliserer "kostnader" ganger rekkevidden "sendt" (B14). Det kalles "matrix multiplikasjon."
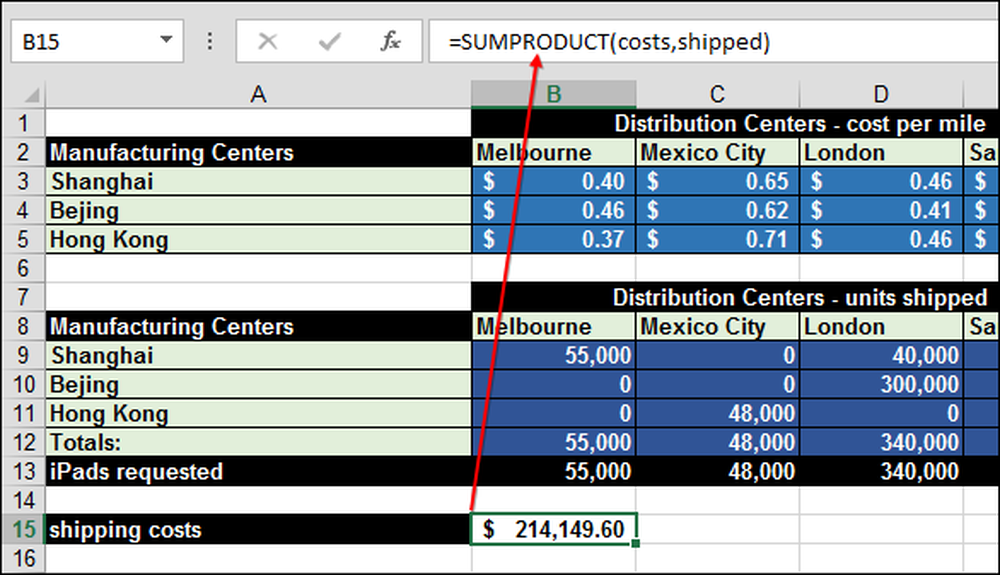
For at SUMPRODUCT skal kunne fungere riktig, må de to matrices - koster og sendes - være i samme størrelse. Du kan omgå denne begrensningen ved å gjøre ekstra kostnader og fraktsøyler og rader med nullverdi slik at arrayene er like store og det ikke er noen innvirkning på de totale kostnadene.
Bruk av Solver
Hvis alt vi hadde å gjøre var å multiplisere matrisene "kostnader" ganger "sendt" det ville ikke være for komplisert, men vi må også håndtere begrensninger der.
Vi må sende hva hver distribusjonssenter krever. Vi legger det konstant inn i løsningen som dette: $ B $ 12: $ E $ 12> = $ B $ 13: $ E $ 13. Dette betyr summen av hva som sendes, dvs. summene i celler $ B $ 12: $ E $ 12, må være større enn eller lik det som hvert distribusjonssenter krever ($ B $ 13: $ E $ 13).

Vi kan ikke sende mer enn vi produserer. Vi skriver disse begrensningene slik: $ F $ 9: $ F $ 11 <= $G$9:$G$11. Put another way, what we ship from each plant $F$9:$F$11 cannot exceed (must be less than or equal to) the capacity of each plant: $G$9:$G$11.
Gå nå til "Data" -menyen og trykk "Solver" -knappen. Hvis "Solver" -knappen ikke er der, må du aktivere tilleggsoppdateringen Solver.
Skriv inn de to begrensningene som er detaljert tidligere, og velg "Sendinger" -området, som er rekkevidden av tall som vi ønsker at Excel skal beregne. Også velg standard algoritmen "Simplex LP" og indikere at vi vil "minimere" cellen C15 ("totale fraktkostnader"), der det står "Set Objective."
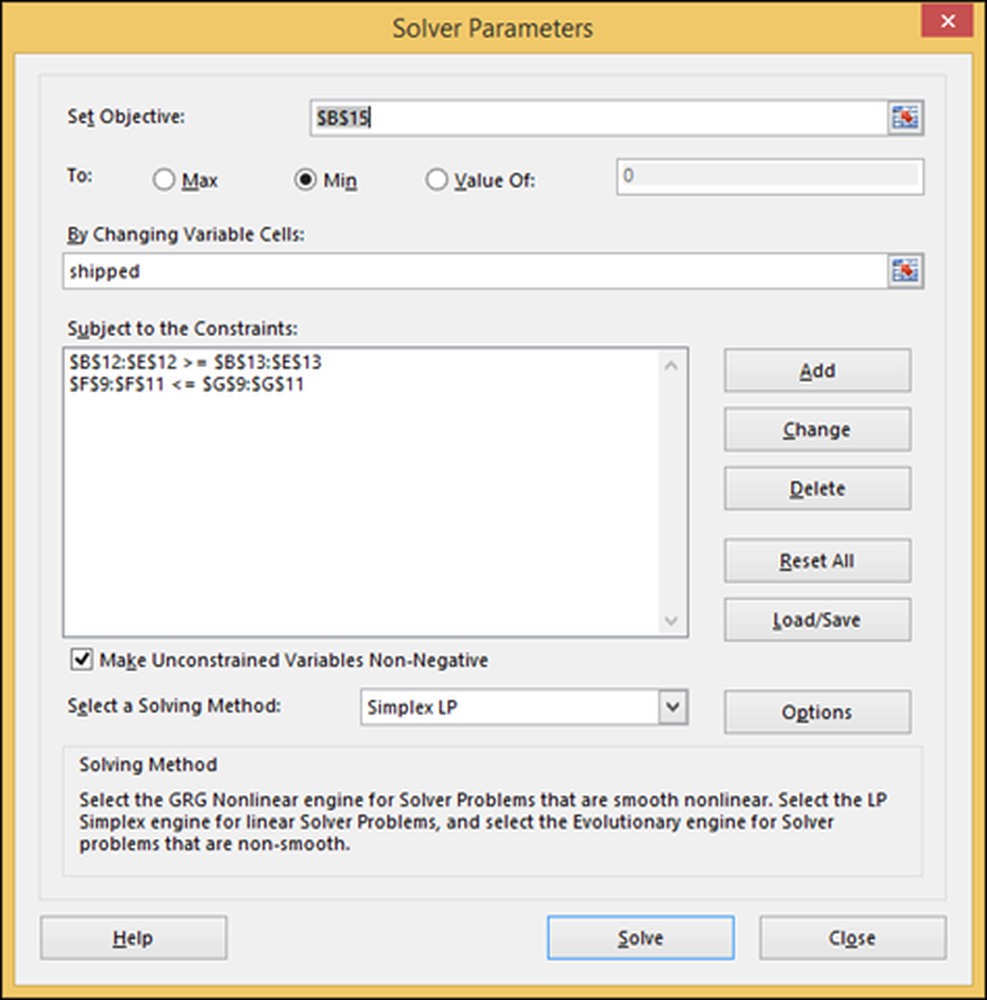
Trykk "Løs" og Excel lagrer resultatene i regnearket, som er det vi ønsker. Du kan også lagre dette slik at du kan leke med andre scenarier.
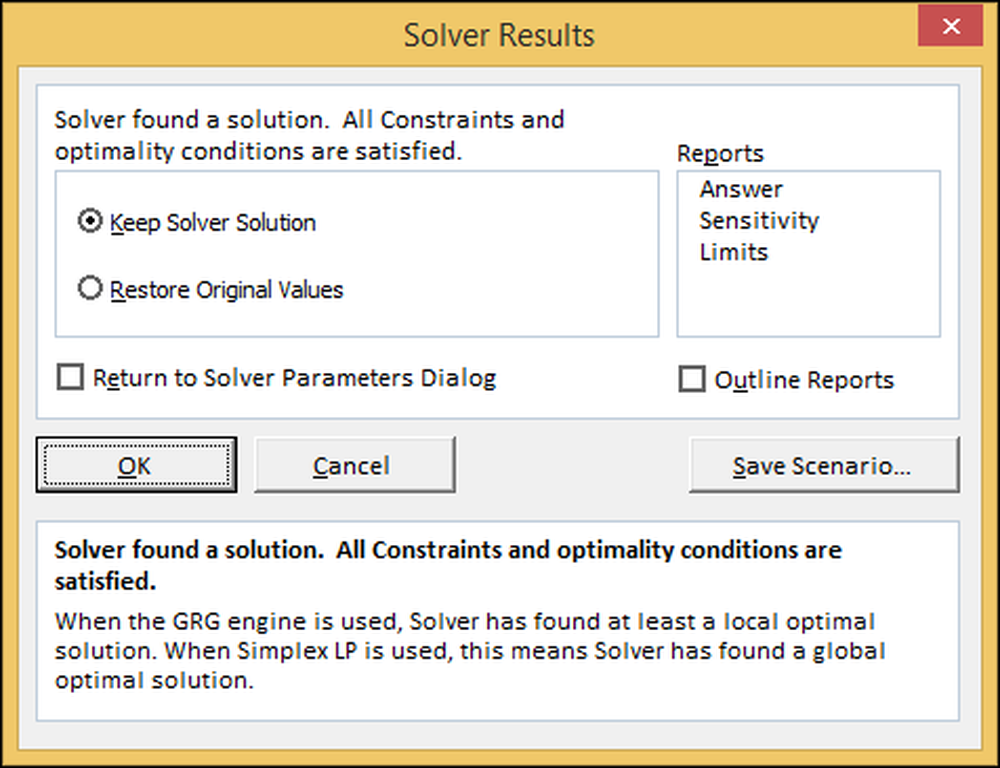
Hvis datamaskinen sier at den ikke kan finne en løsning, har du gjort noe som ikke er logisk, for eksempel kan du ha bedt om flere iPads enn plantene kan produsere.
Her forteller Excel at den fant en løsning. Trykk "OK" for å holde løsningen og gå tilbake til regnearket.
Eksempel: Netto nåverdi
Hvordan bestemmer et selskap om å investere i et nytt prosjekt? Hvis "Netto nåverdi" (NPV) er positiv, vil de investere i den. Dette er en standard tilnærming tatt av de fleste økonomiske analytikere.
For eksempel, antar at Codelco-gruveselskapet ønsker å utvide Andinas kobbergruve. Standardmetoden for å avgjøre om prosjektet skal gå videre er å beregne netto nåverdi. Hvis NPV er større enn null, vil prosjektet være lønnsomt gitt to innganger (1) tid og (2) kapitalkostnad.
På vanlig engelsk betyr kostnaden for kapital hvor mye de pengene ville tjene hvis de bare forlot det i banken. Du bruker kapitalkostnaden til å kalkulere kontantverdier til nåverdi, med andre ord $ 100 om fem år kan være $ 80 i dag.
I det første året er 45 millioner dollar avsatt som kapital for å finansiere prosjektet. Revisorene har fastslått at deres kapitalkostnader er seks prosent.

Når de starter gruvedrift, begynner kontanter å komme inn da selskapet finner og selger kobberet de produserer. Tydeligvis, jo mer de mine, jo flere penger de gjør, og deres prognose viser at kontantstrømmen øker til den når $ 9 millioner per år.
Etter 13 år er NPV $ 3 945 074 USD, så prosjektet vil være lønnsomt. Ifølge finansanalytikere er "tilbakebetalingstiden" 13 år.
Opprette et pivottabell
Et "pivottabell" er i utgangspunktet en rapport. Vi kaller dem pivottabeller fordi du enkelt kan bytte dem en type rapport til en annen uten å måtte lage en helt ny rapport. Så de dreie på plass. La oss vise et grunnleggende eksempel som lærer de grunnleggende konseptene.
Eksempel: Salgsrapporter
Salgsfolk er svært konkurransedyktige (det er en del av å være en selger), så de vil naturligvis vite hvordan de går mot hverandre i slutten av kvartalet og slutten av året, pluss hvor mye provisjonene deres vil bli.
Anta at vi har tre selgere - Carlos, Fred og Julie - alle selger petroleum. Deres salg i dollar per regnskapsår for 2014 er vist i regnearket under.
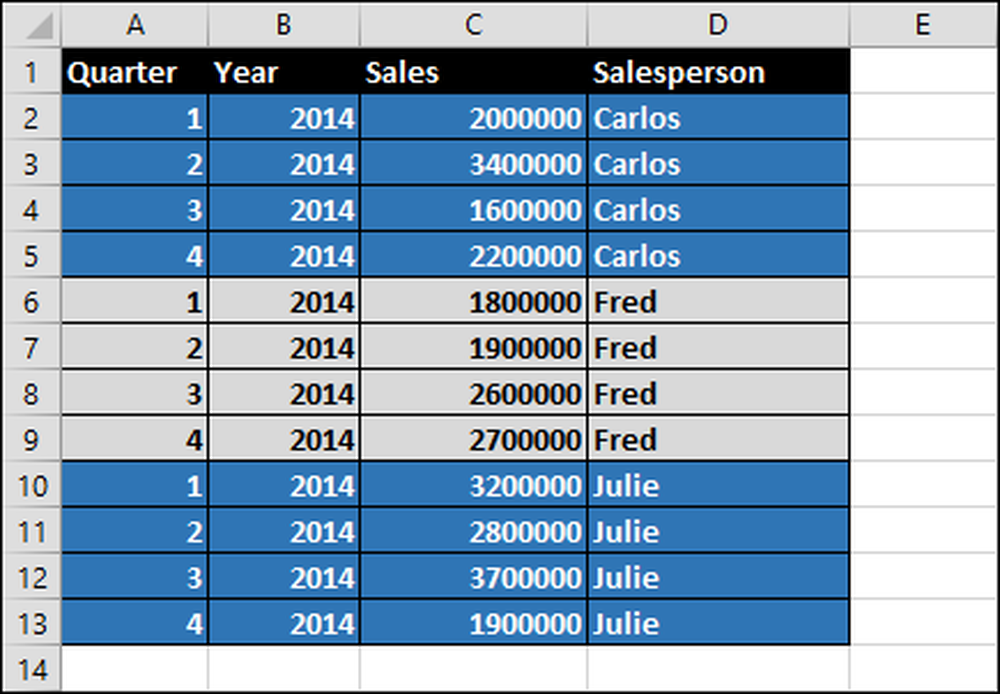
For å generere disse rapportene oppretter vi et pivottabell:
Velg "Insert -> Pivot Table, den er på venstre side av verktøylinjen:
Velg alle rader og kolonner (inkludert selgernavnet) som vist nedenfor:
Dialogboksen for pivottabellen vises til høyre i regnearket.
Hvis vi klikker på alle fire feltene i pivottabelldialogboksen (kvartal, år, salg og selger) legger Excel til en rapport i regnearket som ikke gir mening, men hvorfor?
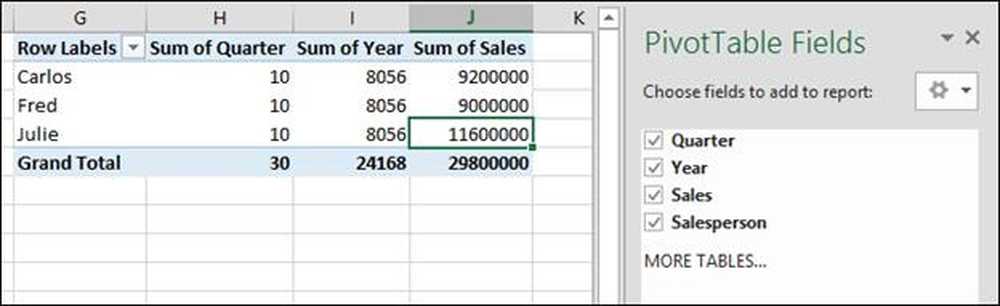
Som du kan se, har vi valgt alle fire feltene som skal legges til rapporten. Excels standardadferd er å gruppere rader ved hjelp av tekstfelt og summere resten av radene.
Her gir det oss summen av 2014 + 2014 + 2014 + 2014 = 24.168, noe som er tull. Det er også gitt summen av kvartalet 1 + 2 + 3 + 4 = 10 * 3 = 3 0. Vi trenger ikke denne informasjonen, så vi fjerner disse feltene for å fjerne dem fra vårt pivottabell.
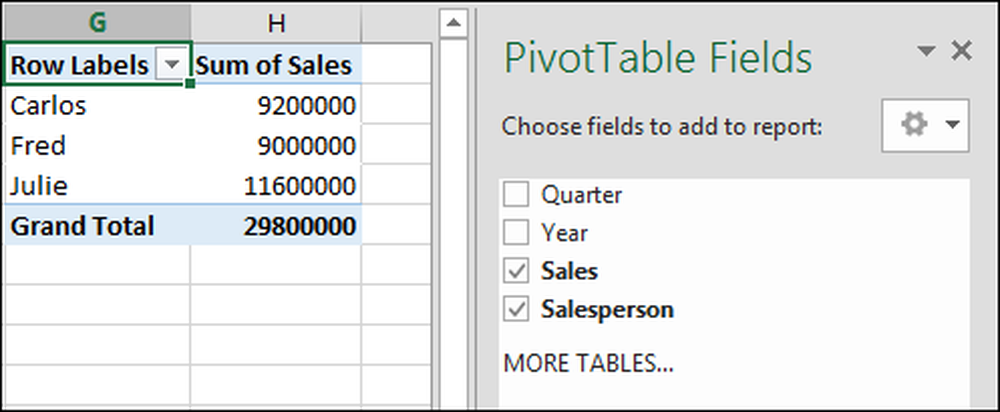
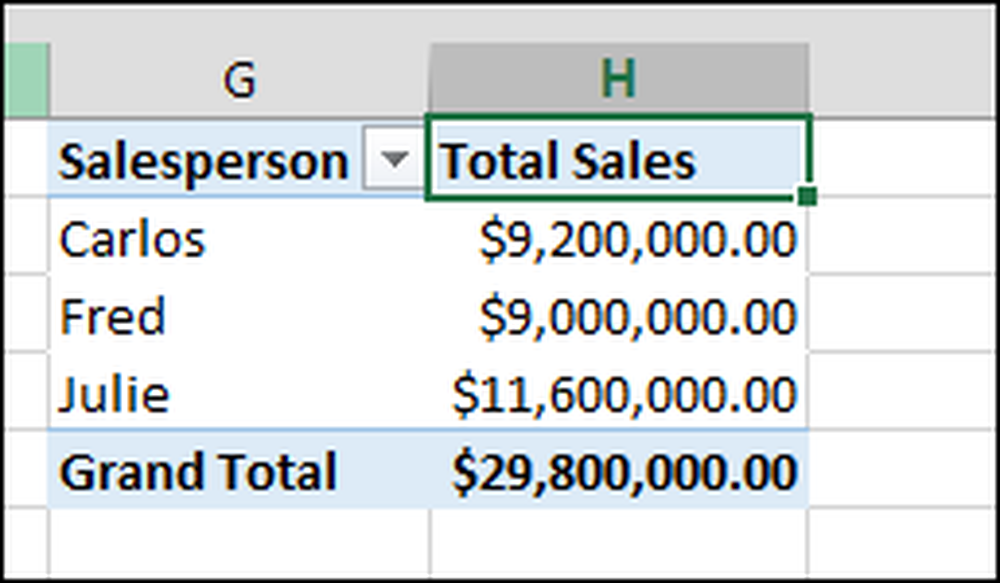
"Sum av salg" (total salg) er imidlertid relevant, så vi skal fikse det.
Eksempel: Salg av selger
Du kan redigere "Sum of Sales" som å si "Total Sales", som er klarere. Du kan også formatere cellene som valuta, akkurat som du ville formatere noen andre celler. Først klikk på "Sum of Sales" og velg "Value Field Settings."

På den resulterende dialogen endrer vi navnet til "Total salg" og klikker deretter "Nummerformat" og endrer det til "Valuta".
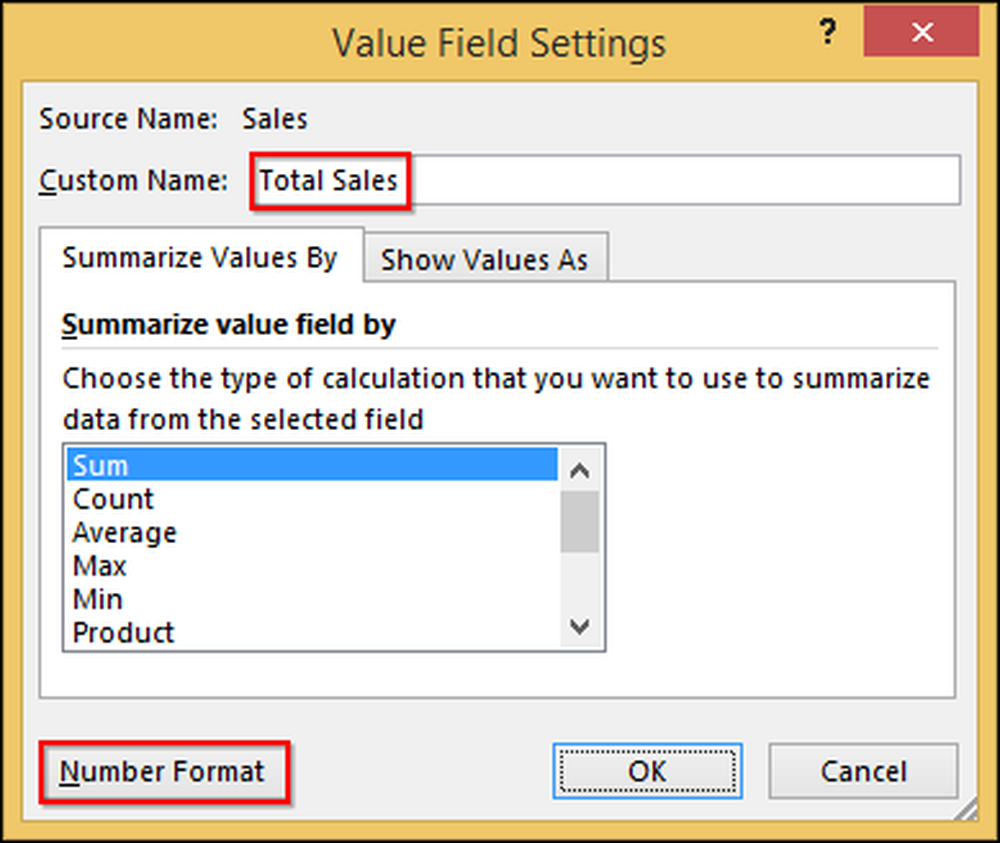
Du kan da se håndarbeidet ditt i pivottabellen:
Eksempel: Salg av selger og kvartal
La oss nå legge til subtotaler for hvert kvartal. For å legge til subtotaler bare venstre-klikk på "Quarter" -feltet og hold og dra det til "rader" -delen. Du kan se resultatet på skjermbildet nedenfor:

Mens vi er på det, la oss fjerne "Sum of Quarter" -verdiene. Bare klikk på pilen og klikk på "Fjern felt". I skjermbildet kan du nå se at vi har lagt til "Quarter" -raden, som bryter ned hver selgeres salg per kvartal.
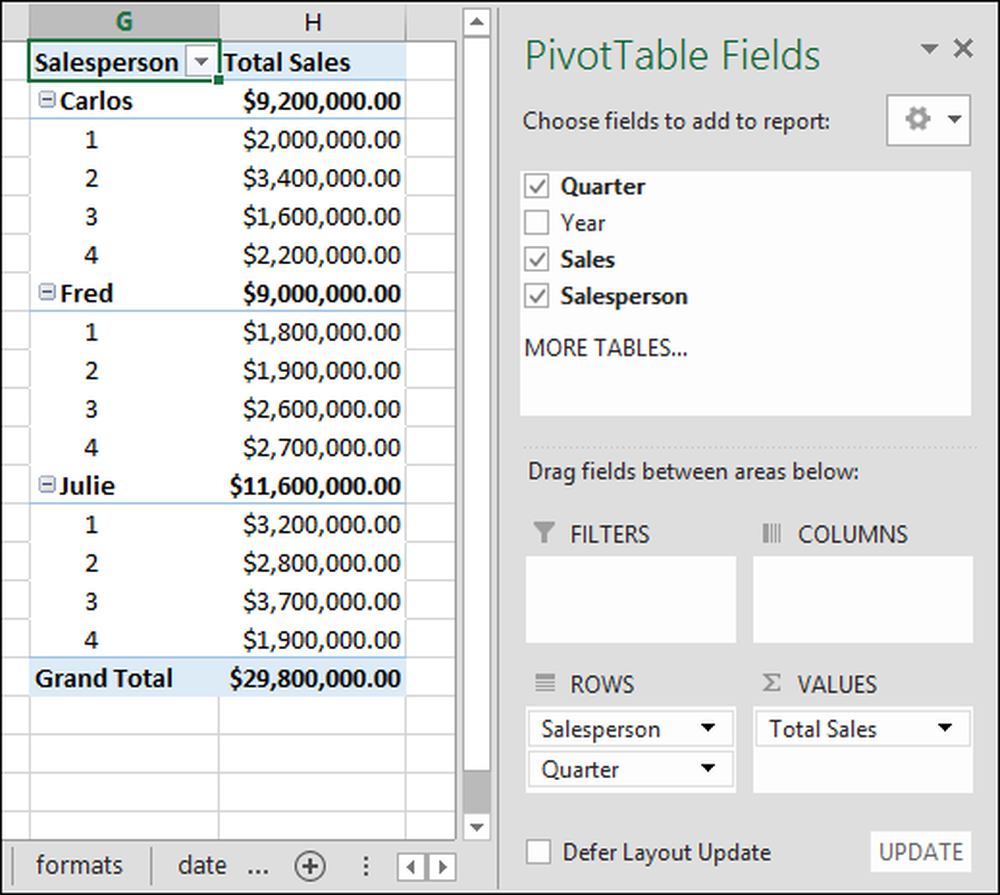
Med disse ferdighetene i tankene kan du nå lage pivottabeller fra dine egne data!
Konklusjon
Innpakning, vi har vist deg noen av funksjonene i Microsoft Excels formler og funksjoner som du kan bruke Microsoft Excel til din virksomhet, akademiske eller andre behov.
Som du har sett, er Microsoft Excel et enormt produkt med så mange funksjoner at de fleste, selv avanserte brukere, ikke kjenner dem alle. Noen kan si at det gjør det komplisert; Vi føler at det er mer omfattende.
Forhåpentligvis, ved å presentere deg mange eksempler på ektefelle, har vi ikke bare demonstrert funksjonene som er tilgjengelige i Microsoft Excel, men har lært deg noe om statistikk, lineær programmering, lage diagrammer, bruk av tilfeldige tall og andre ideer som du nå kan vedta og bruk i skolen din eller hvor du jobber.
Husk at hvis du vil gå tilbake og ta klassen igjen, kan du begynne å friske med leksjon 1!




