Slik beregner du en Z-Score ved hjelp av Microsoft Excel

En Z-Score er en statistisk verdi som forteller deg hvor mange standardavvik en bestemt verdi kommer til å være fra gjennomsnittet av hele datasettet. Du kan bruke AVERAGE- og STDEV.S- eller STDEV.P-formler til å beregne gjennomsnittlig og standardavviket for dataene dine og deretter bruke disse resultatene til å bestemme Z-score for hver verdi.

Hva er en Z-score, og hva gjør funksjonene AVERAGE, STDEV.S og STDEV.P?

En Z-Score er en enkel måte å sammenligne verdier fra to forskjellige datasett. Det er definert som antall standardavvik bort fra det gjennomsnittlige datapunktet ligger. Den generelle formelen ser slik ut:

= (Datapoint-GJENNOMSNITT (datasett)) / STDEV (datasett)

Her er et eksempel for å bidra til å avklare. Si at du ønsket å sammenligne testresultatene fra to algebra-studenter undervist av forskjellige lærere. Du vet at den første studenten fikk 95% på avsluttende eksamen i en klasse, og studenten i den andre klassen fikk 87%.

Ved første øyekast er 95% -graden mer imponerende, men hva om læreren i den andre klassen ga en vanskeligere eksamen? Du kan beregne Z-poengsummen for hver elevs poengsum basert på gjennomsnittspoengene i hver klasse og standardavviket av poengene i hver klasse. Sammenligning av de to studenternes Z-poeng kunne avsløre at studenten med 87% -poenget gjorde det bedre i forhold til resten av klassen enn studenten med 98% -poenget gjorde i forhold til resten av klassen.

Den første statistiske verdien du trenger er "mean" og Excels "AVERAGE" -funksjon beregner den verdien. Den legger ganske enkelt opp alle verdiene i et celleområde og deler den summen av antall celler som inneholder numeriske verdier (det ignorerer tomme celler).

Den andre statistiske verdien vi trenger er "standardavviket" og Excel har to forskjellige funksjoner for å beregne standardavviket på litt forskjellige måter.

Tidligere versjoner av Excel hadde bare "STDEV" -funksjonen, som beregner standardavviket mens du behandler dataene som et "utvalg" av en befolkning. Excel 2010 brøt det inn i to funksjoner som beregner standardavviket:

STDEV.S: Denne funksjonen er identisk med den forrige "STDEV" -funksjonen. Den beregner standardavviket mens du behandler dataene som en "prøve" av en befolkning. En prøve av en befolkning kan være noe som de spesielle myggene samlet for et forskningsprosjekt eller biler som ble satt til side og brukt til å krasje sikkerhetstesting.
STDEV.P: Denne funksjonen beregner standardavviket mens du behandler dataene som hele befolkningen. En hel befolkning ville være noe som alle mygg på jorden eller hver bil i en produksjonsløp av en bestemt modell.

Som du velger, er det basert på datasettet. Forskjellen vil vanligvis være liten, men resultatet av "STDEV.P" -funksjonen vil alltid være mindre enn resultatet av "STDEV.S" -funksjonen for det samme datasettet. Det er en mer konservativ tilnærming å anta at det er mer variasjon i dataene.

La oss se på et eksempel

For vårt eksempel har vi to kolonner ("Verdier" og "Z-Score") og tre "hjelper" -celler for å lagre resultatene av funksjonene "AVERAGE", "STDEV.S" og "STDEV.P". Kolonnen "Verdier" inneholder ti tilfeldige tall som er sentrert rundt 500, og kolonnen "Z-Score" er hvor vi skal beregne Z-score ved hjelp av resultatene lagret i "hjelper" -cellene.

Først skal vi beregne gjennomsnittet av verdiene ved hjelp av funksjonen "AVERAGE". Velg cellen der du vil lagre resultatet av "AVERAGE" -funksjonen.

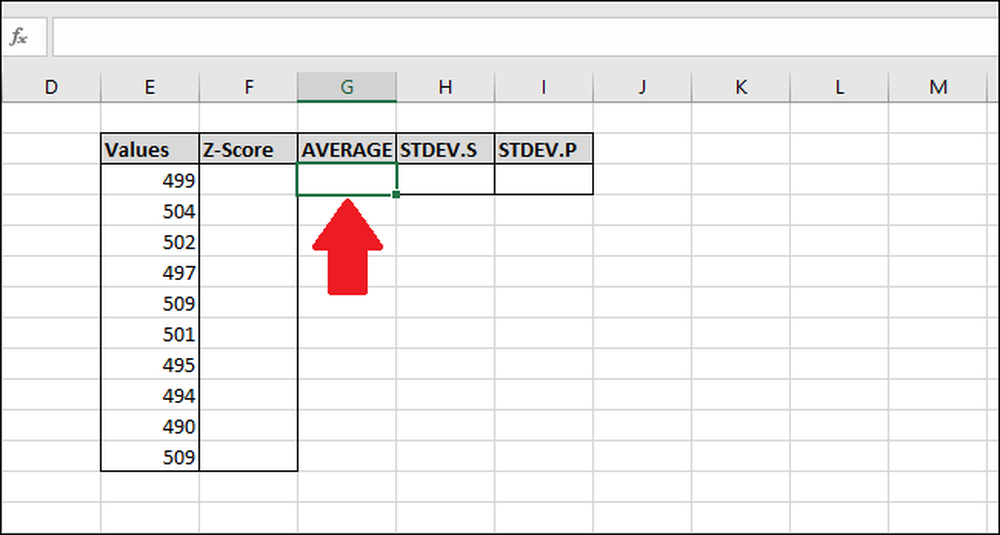
Skriv inn følgende formel og trykk Tast inn -eller bruk menyen "Formler".

= Gjennomsnitt (E2: E13)

For å få tilgang til funksjonen via "Formler" -menyen, velg rullegardinmenyen "Flere funksjoner", velg alternativet "Statistisk", og klikk deretter på "AVERAGE".

I vinduet Funksjonsargumenter velger du alle cellene i kolonnen "Verdier" som input for feltet "Nummer1". Du trenger ikke å bekymre deg for feltet "Number2".

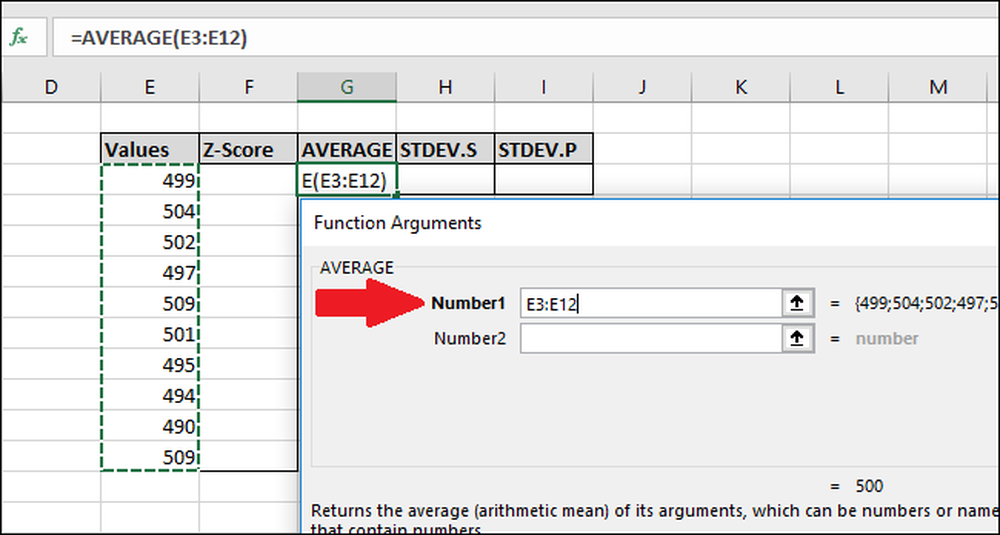
Trykk nå på "OK".

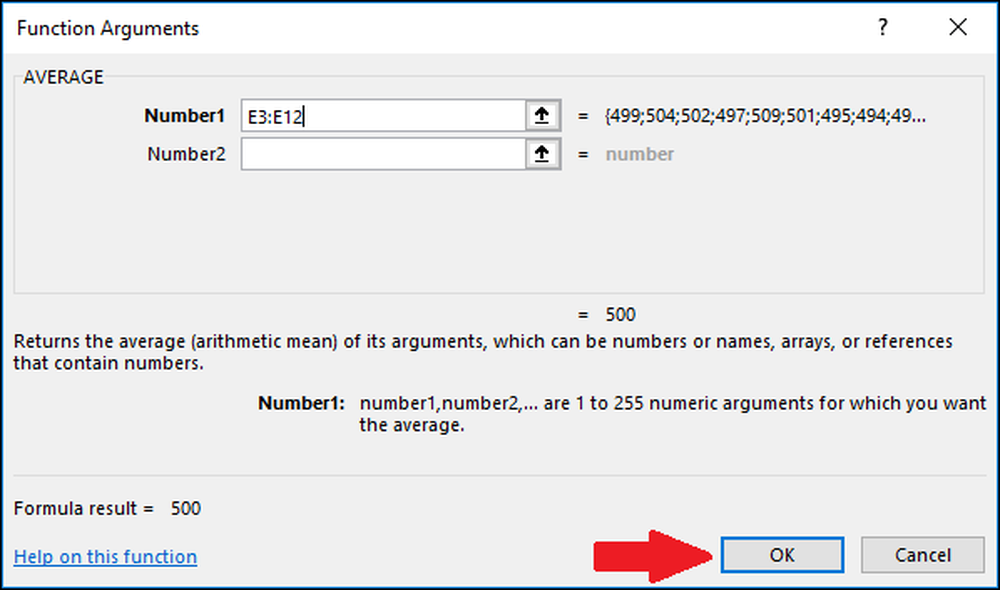
Deretter må vi beregne standardavviket til verdiene ved å bruke enten "STDEV.S" eller "STDEV.P" -funksjonen. I dette eksemplet vil vi vise deg hvordan du beregner begge verdier, starter med "STDEV.S." Velg cellen hvor resultatet blir lagret.

For å beregne standardavviket ved hjelp av funksjonen "STDEV.S", skriv inn denne formelen og trykk Enter (eller få tilgang til den via "Formulas" -menyen).

= STDEV.S (E3: E12)

For å få tilgang til funksjonen via "Formler" -menyen, velg rullegardinmenyen "Flere funksjoner", velg alternativet "Statistisk", bla ned litt, og klikk deretter kommandoen "STDEV.S".

I vinduet Funksjonsargumenter velger du alle cellene i kolonnen "Verdier" som input for feltet "Nummer1". Du trenger heller ikke å bekymre deg om feltet "Number2" her heller.

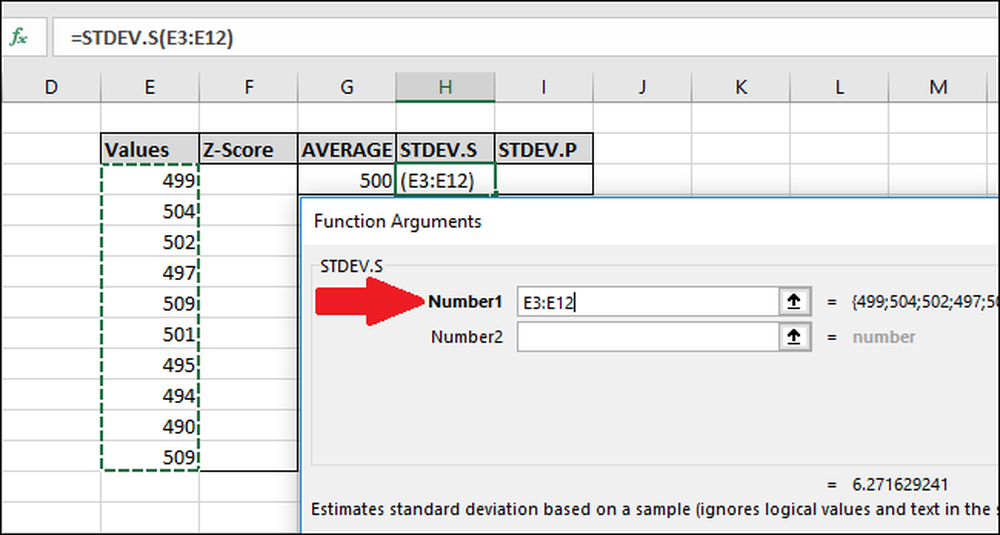
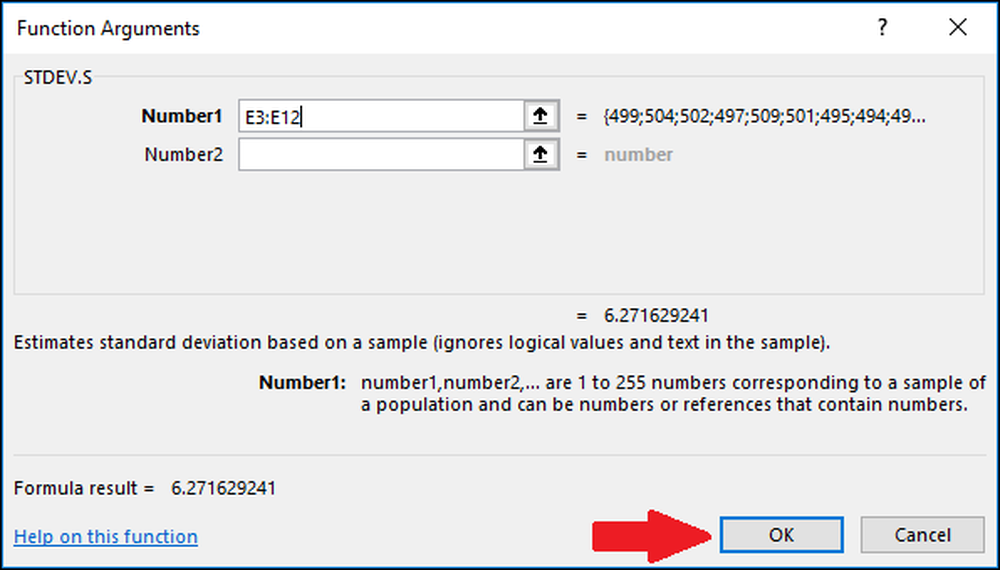
Trykk nå på "OK".

Deretter beregner vi standardavviket ved hjelp av funksjonen "STDEV.P". Velg cellen der resultatet blir lagret.

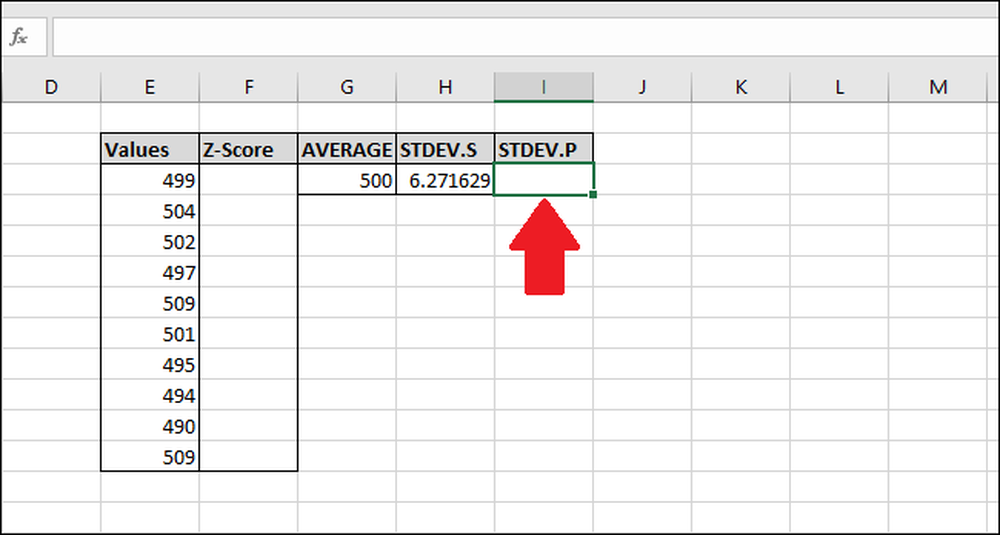
For å beregne standardavviket ved hjelp av "STDEV.P" -funksjonen, skriv inn denne formelen og trykk Enter (eller få tilgang til den via "Formler" -menyen).

= STDEV.P (E3: E12)

For å få tilgang til funksjonen via "Formler" -menyen, velg rullegardinmenyen "Flere funksjoner", velg alternativet "Statistisk", bla ned litt, og klikk deretter på "STDEV.P" -formelen.

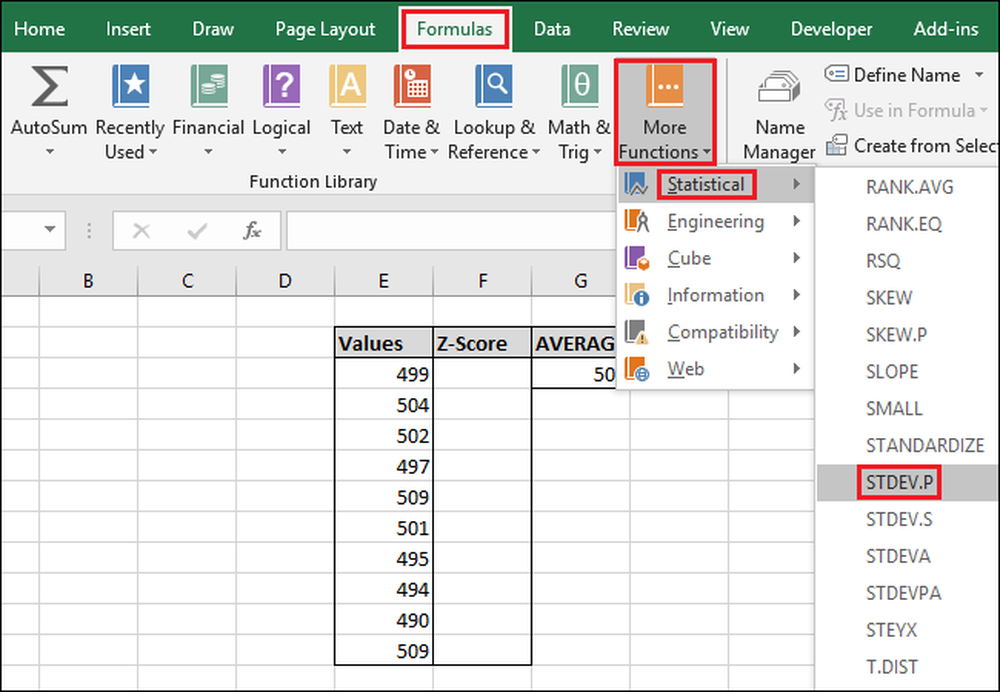
I vinduet Funksjonsargumenter velger du alle cellene i kolonnen "Verdier" som input for feltet "Nummer1". Igjen, du trenger ikke å bekymre deg for "Number2" -feltet.

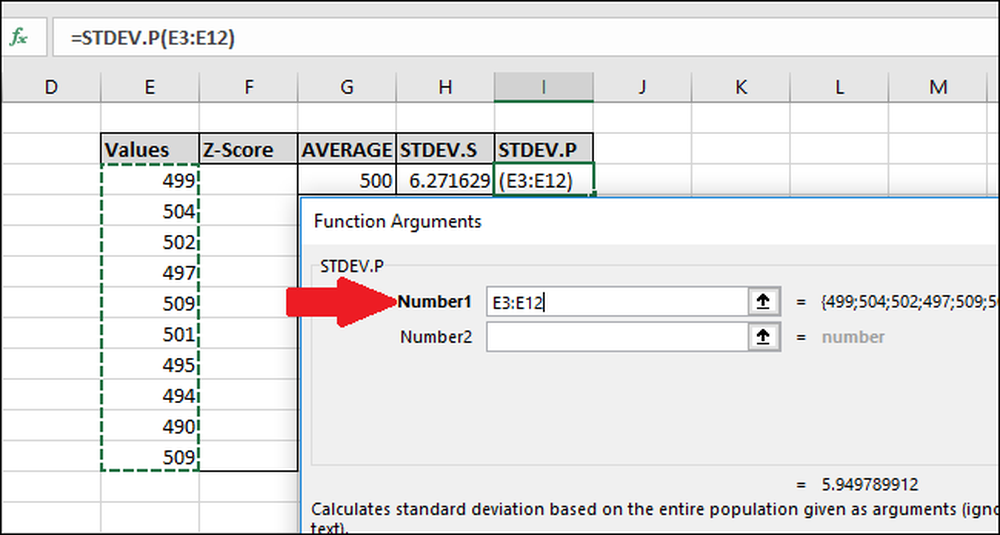
Trykk nå på "OK".

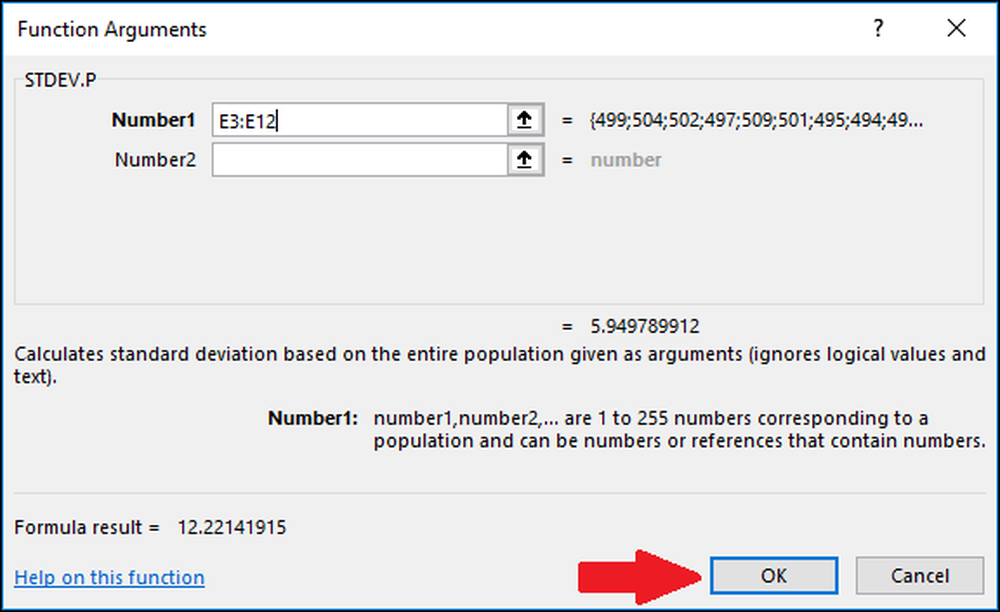
Nå som vi har beregnet gjennomsnittlig og standardavvik for våre data, har vi alt vi trenger for å beregne Z-Score. Vi kan bruke en enkel formel som refererer til cellene som inneholder resultatene av funksjonene "AVERAGE" og "STDEV.S" eller "STDEV.P"..

Velg den første cellen i kolonnen "Z-Score". Vi vil bruke resultatet av "STDEV.S" -funksjonen for dette eksempelet, men du kan også bruke resultatet fra "STDEV.P."

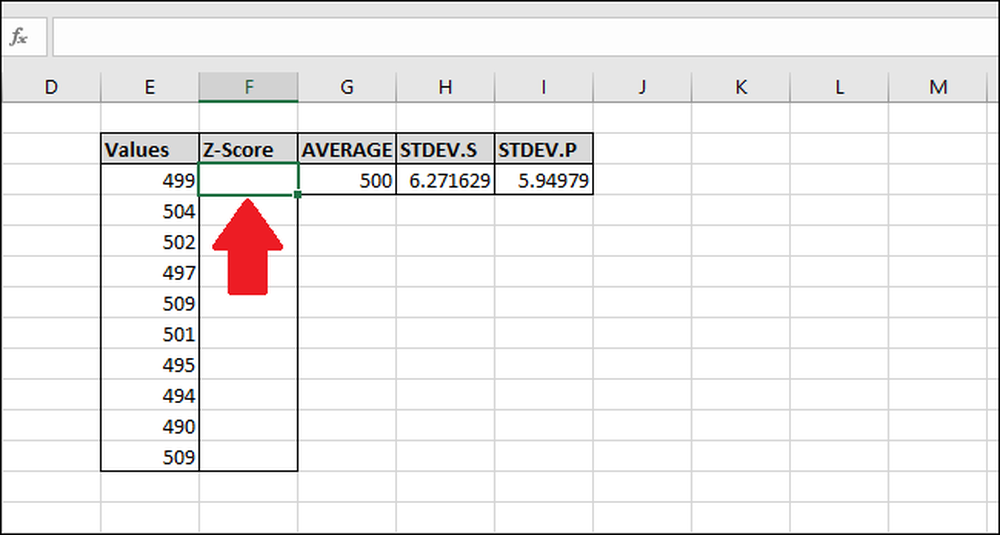
Skriv inn følgende formel og trykk Enter:

= (E3-G $ 3 $) / $ H $ 3

Alternativt kan du bruke følgende trinn for å skrive inn formelen i stedet for å skrive:

Klikk på celle F3 og skriv inn = (
Velg celle E3. (Du kan trykke på venstre pil-tast en gang eller bruk musen)
Skriv minustegnet -
Velg celle G3 og trykk deretter F4 å legge til "$" tegnene for å lage en "absolutt" referanse til cellen (den vil sykle gjennom "G3"> "$G$3 ">" G$3 ">"$G3 ">" G3 "hvis du fortsetter å trykke F4)
Type ) /
Velg celle H3 (eller I3 hvis du bruker "STDEV.P") og trykk F4 å legge til de to "$" tegnene.
trykk enter

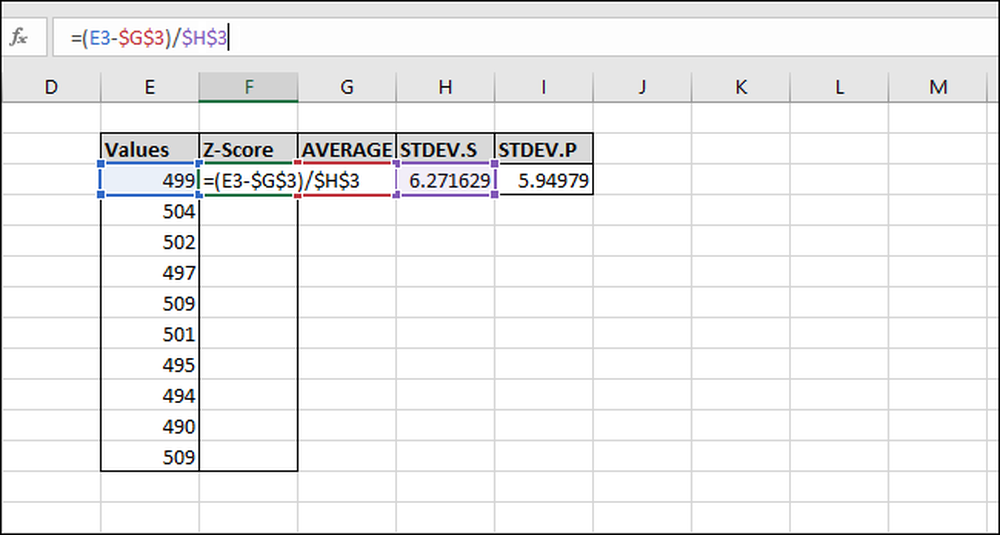
Z-poenget er beregnet for den første verdien. Det er 0,155945 standardavvik under gjennomsnittet. For å sjekke resultatene kan du multiplisere standardavviket ved dette resultatet (6.271629 * -0.15945) og kontrollere at resultatet er lik forskjellen mellom verdien og gjennomsnittet (499-500). Begge resultatene er like, så verdien gir mening.

La oss beregne Z-Scores av resten av verdiene. Marker hele kolonnen Z-Score som starter med cellen som inneholder formelen.

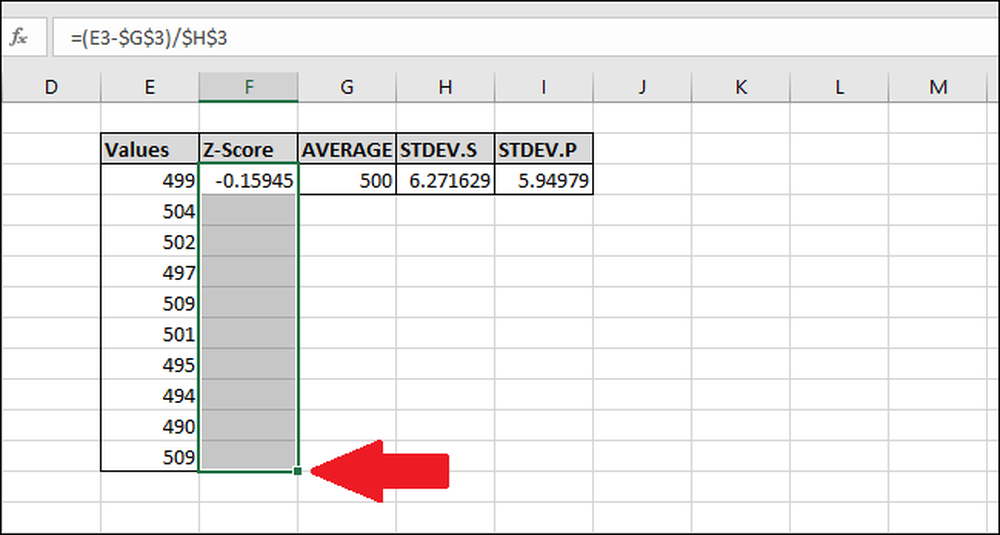
Trykk Ctrl + D, som kopierer formelen i den øverste cellen ned gjennom alle de andre valgte cellene.

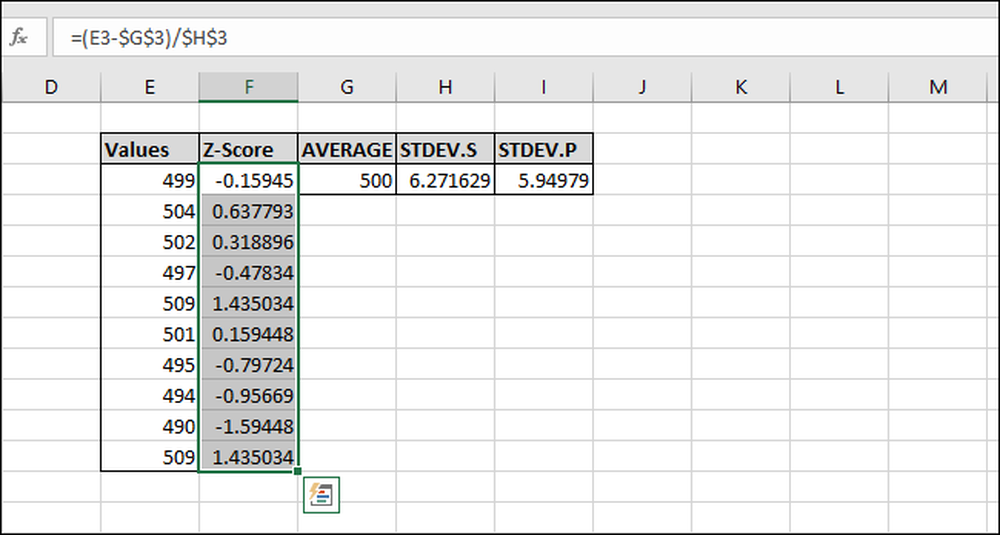
Nå har formelen blitt "fylt ned" til alle cellene, og hver vil alltid referere til de riktige "AVERAGE" og "STDEV.S" eller "STDEV.P" -cellene på grunn av "$" tegnene. Hvis du får feil, gå tilbake og kontroller at "$" -tegnene er inkludert i formelen du skrev inn.

Beregning av Z-score uten bruk av "Hjelper" -celler

Hjelperceller lagrer et resultat, som de som lagrer resultatene av funksjonene "AVERAGE", "STDEV.S" og "STDEV.P". De kan være nyttige, men er ikke alltid nødvendige. Du kan hoppe over dem helt når du beregner en Z-Score ved å bruke følgende generelle formler, i stedet.

Her er en som bruker funksjonen "STDEV.S":

= (Value-gjennomsnitt (verdier)) / STDEV.S (verdier)

Og en som bruker "STEV.P" -funksjonen:

= (Value-gjennomsnitt (verdier)) / STDEV.P (verdier)

Når du går inn i cellelinjene for "Verdiene" i funksjonene, må du legge til absolutte referanser ("$" ved hjelp av F4) slik at når du fyller ned, beregner du ikke gjennomsnittet eller standardavviket i et annet område av celler i hver formel.

Hvis du har et stort datasett, kan det være mer effektivt å bruke hjelperceller fordi det ikke beregner resultatet av funksjonene "AVERAGE" og "STDEV.S" eller "STDEV.P" hver gang, sparer prosessorressurser og Fremskynde tiden det tar å beregne resultatene.

Også "$ G $ 3" tar færre byte å lagre og mindre RAM å laste enn "AVERAGE ($ E $ 3: $ E $ 12).". Dette er viktig fordi standard 32-biters versjon av Excel er begrenset til 2 GB RAM (64-bits versjonen har ingen begrensninger på hvor mye RAM som kan brukes).